Good Morning,
We hope that you and your family are well! September’s Monthly Focus is about pricing with minimum hypotheses and no big computational effort.
A powerful tool
Static replication is a tool that has proven its applicability to a wide range of problems such as static hedging, design of synthetic products, and valuation.
This method is an attempt to mimic the payoff of a given derivative instrument. It involves decomposing the product into components for which market prices and bid-ask spreads are often better known such as zero-coupon, forwards, and vanilla options.
This approach has many advantages. For example, for hedging purposes, it allows avoiding the huge transaction costs involved in using the classical dynamic hedging approach. Static replication is also a powerful tool to get a market price for structured products.
Model-free pricing
The static replication approach in valuing structured products does not require to make restrictive assumptions, as for other pricing models. This model-free pricing technique makes no assumptions beyond those of market conditions and available data. The resulting prices generally reflect more precisely the true costs compared to theoretical pricing models.
LexiFi’s Static Replication algorithm automatically finds a combination of calls and puts replicating the payoff of any product with multiple cash flows, depending only on one underlying observed at one fixing date. Hence, product prices can be simply computed by combining individual calls and puts.
The implementation of this method in LexiFi is possible thanks to LexiFi’s Algebraic representation of contract payoffs which exhaustively models product definitions.
The screenshot below, from the LexiFi Web application, illustrates a payoff decomposition result automatically computed by LexiFi’s Static Replication function.
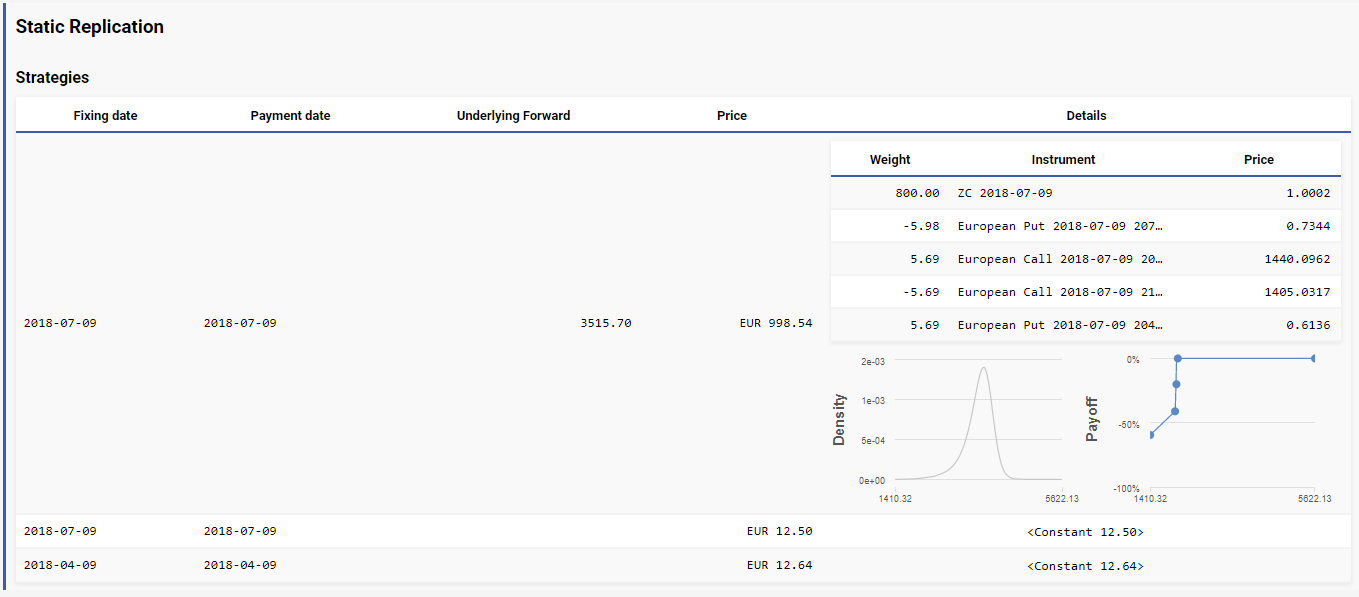
Can we extend this approach to the multi-dimensional case?
Many real-life products tend to be more complex: product cashflows do not always depend on a single fixing per cashflow. Therefore, we had to extend the one-dimensional approach to a multi-dimensional one!
Concretely, we decompose the contract into cashflows with LexiFi’s algebraic representation; then, we price each cashflow using the density of the underlying and correlation structures.
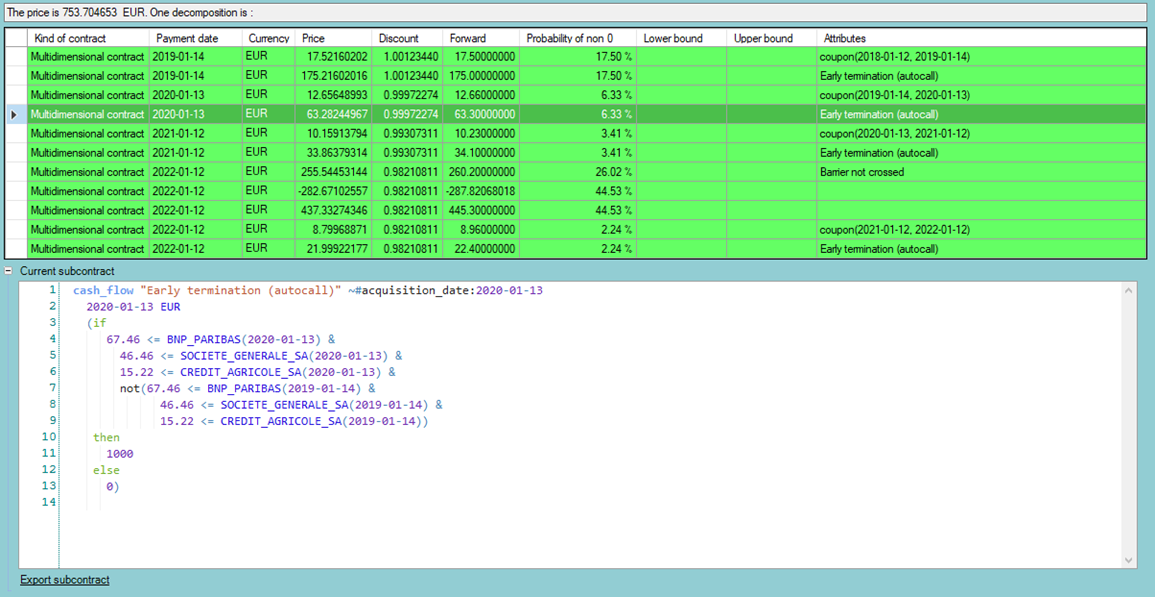
The multi-dimensional static replication results are illustrated below using LexiFi Apropos (the static decomposition inspector page).
Using correlation structures spoils the “model-free” aspect that we had in the one-dimensional approach. Yet, this multi-dimensional approach still satisfies the objective to make the least possible assumptions. The end result is a price range that serves as an indicator for pricing a product or hedging a position, we tell you more about this in the next section!
Why settle for a price when you can get bounds?
Finding the right price for complex structured products is not always straightforward. Modeling and calibrating sometimes lead to different prices on the same payoff.
This inconsistency makes it interesting to use the multi-dimensional static replication approach to obtain price boundaries.
Research on these boundaries falls within a broad topic called Optimal Transport. Its application is particularly dynamic in the quantitative finance field and is known as the Martingale Optimal Transport problem.
A major reference on this topic is Pierre Henry-Labordere’s book on Model-free hedging.
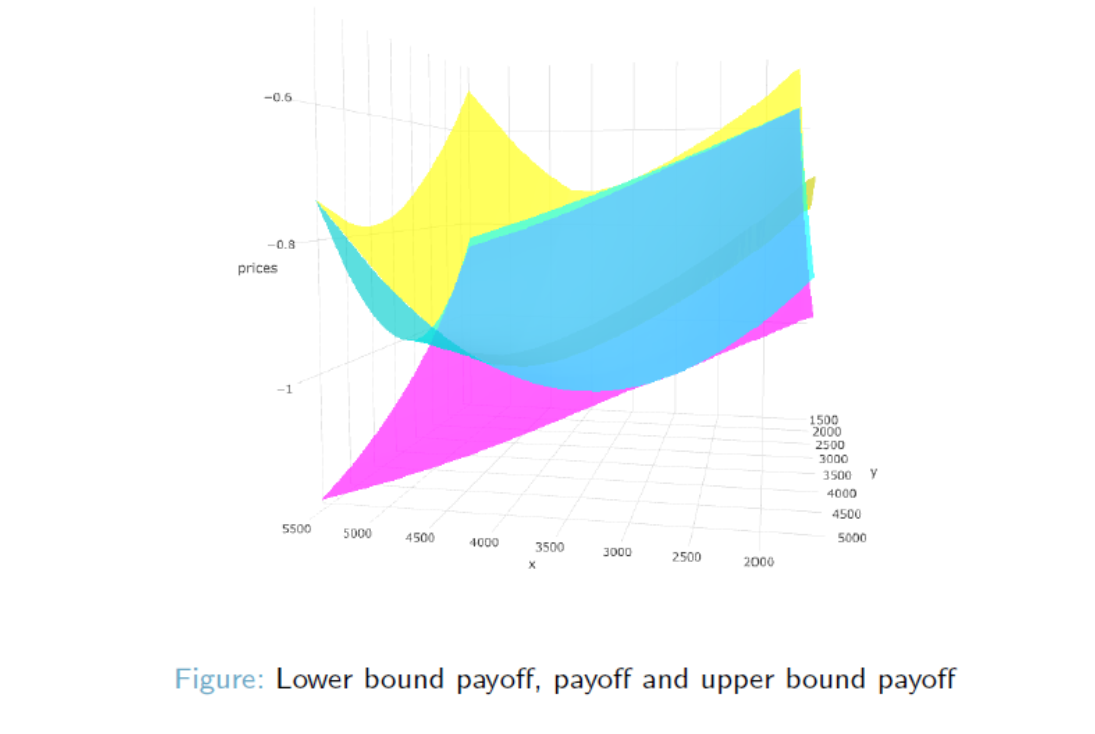
LexiFi quants and devs have implemented multiple solutions to solve the Martingale Optimal Transport problem. The optimal boundary approach is coming soon in LexiFi application. Below is a visual taste of what boundary results would look like in LexiFi Apropos!
Collective intelligence
Research on optimal boundaries is an active topic in the quantitative finance field. Recent advances in Martingale optimal transport problem have enabled LexiFi to provide boundaries for a high dimension of underlyings.
This was in particular thanks to the numerical method exposed in the PhD of Hadrien De March.
Another recent improvement on this subject is the incorporation of a utility function and indifference price on Marco Frittelli and Alessandro Doldi’s work.
Their research also integrates risk measures based on the pioneering work of Philippe Artzner, Freddy Delbaen, Jean-Marc Eber and, David Heath on the so-called Coherent Measures of Risk.