Financial modeling with jump processes is a fully explored domain. We present in this post some of the theoretical aspects of Lévy processes.
We also expose a subset of jump diffusion models available into LexiFi Apropos.
Underlying dynamics, European call pricing and calibration procedures are developed for the Merton and Bates models.
For the sake of clarity, some theoretical aspects and figures are hidden, don’t hesitate to expand them for having more information.
<h2>Element of stochastic calculus</h2>
<p>
In this section, we recall some key points on the extension to discontinuous processes (Itô formula, measure theory, ... ).
we also present Lévy processes (Lévy-Itô decomposition, Lévy-Khintchine representation, ...).
The reader can expand/collapse for more information
</p>
<div id="calsto">
<h3>Extension to discontinuous processes</h3>
<h4>Generalised Itô formula</h4>
<p>
Let $ (X_t)_{t\in\mathbb{R}^+} $ be a cadlag (right-continuity and left limits) process such that $X$ is a continuous semi-martingale and $f$ a twice differentiable function.
Continuous Itô formula:
\[ f(X_{t}) = f(X_{0}) + \int\limits_{0}^{t} {f'(X_{s}) dX_{s} } + \frac{1}{2} \int\limits_{0}^{t} {f''(X_{s}) d \left[ X \right]_{s} } \]
</p>
<p>
Generalised Itô formula:
Let $ X $ be a cadlag process.
\begin{align*}
f(X_{t}) = f(X_{0}) & + \displaystyle \int\limits_{0}^{t} {f'(X_{s^{-}}) dX_{s} } +
\frac{1}{2} \int\limits_{0}^{t} {f''(X_{s^-}) d \left[ X \right]_{s} } \\
& + \displaystyle \sum_{s \le t} {\left[ \triangle f(X_{s}) - f'(X_{s^{-}}) \triangle X_{s^{-}} - \frac{1}{2} f''(X_{s^-}) \triangle X_{s}^{2} \right]}
\end{align*}
with
<ul>
<li> $ X_{t^{-}} = \displaystyle \lim_{s \to t \atop s < t} X_s $ </li>
<li> $ \triangle X_t = X_t - X_{t^{-}} $ </li>
<li> $ \displaystyle \sum_{s \le t} \triangle X_s = \displaystyle \sum_{ \{ t_i , 0 \le t_i \le t \;\; and \;\; \triangle X_{t_i} \neq 0 \} } \triangle X_{t_i} $
such that $ \{ t_i , 0 \le t_i \le t $ and $ \triangle X_{t_i} \neq 0 \} $ is countable </li>
</ul>
</p>
<h4>Splitting: continuous/discontinuous processes</h4>
<p>
Decomposition (continuous and discontinuous):
\[ X = \underbrace{X^{c}}_{continuous \; part} + \underbrace{X^{d}}_{discontinuous \; part} = X^{c} + \displaystyle \sum_{s \le .} \triangle X_{s} \]
The quadratic covariation between two processes is defined by:
\[ \left[ X,Y \right]_{t} = \displaystyle \lim_{ \left| \sigma_{n} \right| \to 0} \sum_{i=1}^{n} (X_{t_i} - X_{t_{i-1}}) (Y_{t_i} - Y_{t_{i-1}}) \]
with $ \left| \sigma_{n} \right| = \sup \{ t_i -t_{i-1} \forall i \in 1,...,n \} $
and $ \sigma_n = \{ t_0 = 0 < ... < t_n = t \} $ a subdivision of $ [ 0 ; t ] $ (size n + 1).
<br />We expose two interesting features:
<ul>
<li> $ [X,Y]_{t}^{c} = [X,Y]_{t} - \displaystyle \sum_{s \le t} \triangle X_{s} \triangle Y_{s} = [X^{c},Y^{c}]_{t} $ </li>
<li> $ d X_t = d X_t^c + \triangle X_t $ </li>
</ul>
</p>
<h3> Lévy process </h3>
<h4> Definition </h4>
<p>
Let $X$ be a stochastic process. $X$ is a Lévy process if
<ul>
<li> $X_0 = 0$ and $X$ cadlag process </li>
<li> $X$ has independent and stationary increments </li>
</ul>
Two important features are:
<ul>
<li> $X$ is continuous in probability: $\forall \epsilon \in \mathbb{R}^{+}, \displaystyle \lim_{s \rightarrow 0} \mathbb{P} ( |X_{s+t} - X_t| > \epsilon ) = 0 $ </li>
<li> $X$ has no jump at a deterministic time: $ \forall t \in \mathbb{R}^+, \mathbb{P} (X_{t^-} = X_t) = 1 $ </li>
</ul>
<br /> Remark: If $X$ is a continuous Lévy process, it can be written as follow:
<br /> $ X_t = \gamma t + A W_t $ with $\gamma \in \mathbb{R}^d $,$W$ a d-dimensional Brownian motion and $A$ a positive semi-definite matrix.
<h4>Probability measure</h4>
Let $ (\Omega, P, \mathcal{F}) $ be a probability space and $(E, \varepsilon)$ a measurable set.
<br /> <strong> Random measure: </strong>
<br /> $M$: $\Omega \times \varepsilon \rightarrow \mathbb{R}$ is a random measure if
<ul>
<li>$\forall \omega \in \Omega$, $M(\omega,\cdot)$ is a measure on $\varepsilon$.</li>
<li>$\forall A \in \varepsilon$, $M(\cdot,A)$ is measurable.</li>
</ul>
<br /> <strong> Poisson random measure: </strong>
<br /> Let $\mu$ be a measure on $(E, \varepsilon)$, $M$: $\Omega \times \varepsilon \rightarrow \mathbb{R}$ is a Poisson random measure with intensity $\mu$ if
<ul>
<li>$\forall A \in \varepsilon$ with $\mu(A) < +\infty$ , $M(\cdot,A)$ follows a Poisson law with intensity $ \mu(A)$ $( \, = E[M(\cdot,A)] \,\,)$. </li>
<li>$\forall (A_1, \ldots, A_n) \in \epsilon^n$ separated sets, $M(\cdot,A_1), \ldots, M(\cdot,A_n)$ are independents. </li>
</ul>
<br /> <strong> Jump measure: </strong>
<br /> Let X be a cadlag process with value in $\mathbb{R}^d$.
The jump measure of $X$ is a random measure on $ [0;\infty) \times \mathbb{R}^d$ defined by:
<br /> $ \forall A \in ( \mathbb{R}^+ \times \mathbb{R}^d) $, $ J_X(A) = \# \{t:\Delta X_t \neq 0$ and $(t,\Delta X_t) \in A \} $
<br /> <br /> Property: A jump measure of a Lévy process is a Poisson measure.
<br /> Remark: A jump measure of the set $([t1,t2],B)$ corresponds to the number of jump between $t1$ and $t2$ with a size include in $B$.
<br /> <br /> <strong> Lévy measure: </strong>
<br /> Let $X$ be a Lévy process with value in $\mathbb{R}^d$.
The Lévy measure of $X$ is a measure defined by:
<br /> $ \forall A \in \mathcal{B} (\mathbb{R}^d)$, $\, \nu(A) = \mathbb{E}[ \# \{ t \in [0,1]: \Delta X_t \neq 0$ and $\Delta X_t \in A \} ]$
<h4>Lévy-Itô decomposition</h3>
Let $X$ be a Lévy process with value in $\mathbb{R}^d$ and the Lévy measure $\nu$ then
<ul>
<li> Its jump measure $ J_X $ is a Poisson random measure on $[0;\infty)$ with intensity $dt \times \nu$ </li>
<li> Its Lévy measure verifies $ \displaystyle \int\limits_{\mathbb{R}^d} (\|x\|^2)\wedge 1) \nu(dx) < \infty $ </li>
<li> There exists $\gamma \in \mathbb{R}^d$ and a d-dimensional brownian motion $B$ with covariance matrix $A$ such that:
\begin{align*}
X_t = & \gamma t + B_t + N_t + M_t \\
N_t = & \displaystyle \int\limits_{ |x| > 1, s \in [0,t] } x J_X(ds \times dx) \\
M_t = & \displaystyle \int\limits_{ 0 < |x| < 1, s \in [0,t] } x \tilde{J}_X(ds \times dx)
= \displaystyle \int\limits_{ 0 < |x| < 1, s \in [0,t] } x [J_X(ds \times dx) - \nu(dx)ds]
\end{align*} </li>
</ul>
<br /> The process $N$ corresponds to a composed Poisson process with jump greater than 1.
<br /> The process $M$ corresponds to a composed and compensated Poisson process with jump lower than 1.
<br /> We remove the mean of small jumps so that the integral will be computable (can be infinite).
Let's note that $M$ is a martingale.
<br /> We only have to define a Lévy process using the following tuple: $(A, \nu, \gamma)$. This is called the characteristic triplet.
<br /> Remark:
We find the commonly used formula for $X$ a continuous Lévy process. The characteristic triplet is $(A, 0, \gamma )$.
We can rewrite the previous decomposition with $ \epsilon \in \mathbb{R} $:
\begin{align*}
N_t = & \displaystyle \int\limits_{ |x| > \epsilon, s \in [0,t] } x J_X(ds \times dx) \\
M_t = & \displaystyle \int\limits_{ 0 < |x| < \epsilon, s \in [0,t] } x \tilde{J}_X(ds \times dx)
= \displaystyle \int\limits_{ 0 < |x| < \epsilon, s \in [0,t] } x [J_X(ds \times dx) - \nu(dx)ds] \\
\gamma^\epsilon = & \gamma - \displaystyle \int\limits_{ \epsilon < |x| < 1, s \in [0,t] } x \nu(dx)ds
\end{align*}
We can compute the $\displaystyle \lim_{\epsilon \rightarrow 0} $ in the decomposition formula.
Lévy-Khintchine representation
Let $X$ be a Lévy process with characteristic triplet $(A, \nu, \gamma)$. The characteristic function is: \[ \mathbb{E} [ e^{iuX_t} ] = exp \left\{\, t \, \big[\, i\, \gamma\, u - \frac{A u^2}{2} + \displaystyle \int\limits_{\mathbb{R}} ( e^{i \, u \, x} - 1 - i \, u \, x 1_{|x| \le 1} ) \nu (dx) \,\big]\, \right\} \]Exponential formula
Let M be a Poisson random measure on $(E, \varepsilon)$ with intensity $\mu$, $B \in \varepsilon$ and f a measurable function such that $\displaystyle \int\limits_{B} |e^{f(x)} - 1| \mu(dx) < \infty$. The following equality holds: \[ \mathbb{E} \left[e^{ \, \int\limits_{B} f(x) M(dx) \,}\right] = exp \left[ \, \int\limits_{B} ( e^{f(x)} - 1 ) \mu(dx)\,\right] \]Exponential Lévy process
Let $X$ be a Lévy process with triplet $ (\sigma, \nu, \gamma) $. Let's note $Y = e^{X} $. We can apply the generalise Itô formula for semi-martingale:\begin{align*} Y_t = & e^{X_0} + \int\limits_0^t e^{X_{s^-}} d X_s + \frac{1}{2} \int\limits_0^t e^{X_{s^-}} d [X_s]
- \displaystyle \sum\limits_{s \le t} [ \Delta e^{X_s} - e^{X_{s^-}}\Delta {X_s} , ] \
= & 1 + \int\limits_0^t Y_{s^-} dX_s + \frac{1}{2} \int\limits_0^t Y_{s^-} \sigma^2 ds - \displaystyle \sum\limits_{s \le t} [ e^{X_{s^-} + \Delta X_s} - e^{X_{s^-}} - e^{X_{s^-}} \Delta X_s ] \
= & 1 + \int\limits_0^t Y_{s^-} dX_s + \frac{1}{2} \int\limits_0^t Y_{s^-} \sigma^2 ds - \displaystyle \sum\limits_{s \le t} Y_{s^-} [ e^{\Delta X_s} - 1 - \Delta X_s ] \
= & 1 + \int\limits_0^t Y_{s^-} dX_s + \frac{1}{2} \int\limits_0^t Y_{s^-} \sigma^2 ds - \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1 - x ] J_X (ds \times dx) \
Y_t = & 1 + \int\limits_0^t Y_{s^-} [ \gamma + \frac{\sigma^2}{2}] ds + \int\limits_0^t Y_{s^-} \sigma dW_s \
& + \int\limits_0^t Y_{s^-} \int\limits_{\mathbb{R}} x J_X (ds \times dx)
- \int\limits_0^t Y_{s^-} \int\limits_{-1}^{1} x \nu (dx) ds \
& + \int\limits_0^t \int\limits_{\mathbb{R}} [ Y_{s^-} [ e^{x} - 1 - x ] J_X (ds \times dx) \end{align*}
We can split the process in a martingale part and a finite variation part. We have: \begin{align*} Y_t = & 1 + \int\limits_0^t Y_{s^-} [ \gamma + \frac{\sigma^2}{2}] ds + \int\limits_0^t Y_{s^-} \sigma dW_s
- \int\limits_0^t Y_{s^-} \int\limits_{-1}^{1} x \nu (dx) ds \
& + \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1] J_X (ds \times dx)
- \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1] \nu (dx) ds
- \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1] \nu (dx) ds \
Y_t = & 1 + \int\limits_0^t Y_{s^-} [ \gamma + \frac{\sigma^2}{2}] ds + \int\limits_0^t Y_{s^-} \sigma dW_s - \int\limits_0^t Y_{s^-} \int\limits_{-1}^{1} x \nu (dx) ds \
& + \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1 ] \tilde{J}_X (ds \times dx)
- \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1] \nu (dx) ds \
Y_t = & 1 + \int\limits_0^t Y_{s^-} [ \gamma + \frac{\sigma^2}{2}] ds + \int\limits_0^t Y_{s^-} \sigma dW_s \
& + \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1 ] \tilde{J}_X (ds \times dx) - \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1 - x 1_{|x| < 1}] \nu (dx) ds \end{align*}
We therefore have $ Y = e^{X} = A + M $, with $ A $ and $ M $ defined as follows:
\begin{align*}
\forall t \in \mathbb{R}^+, A_t = & \int\limits_0^t Y_{s^-} [ \gamma + \frac{\sigma^2}{2} ] ds
+ \int\limits_0^t \int\limits_{\mathbb{R}} [ e^{x} - 1 - x 1_{|x| < 1}] \nu (dx) ] ds \
\forall t \in \mathbb{R}^+, M_t = & 1 + \int\limits_0^t Y_{s^-} \sigma dW_s
+ \int\limits_0^t \int\limits_{\mathbb{R}} Y_{s^-} [ e^{x} - 1 ] \tilde{J}_X (ds \times dx)
\end{align*}
Generality on exponential Lévy models
We develop in this section a general dynamic for exp-Lévy models. We expose a valuation method using partial integro-differential equation (PIDE). The reader can expand/collapse for more information.
Underlying dynamic
Let $S_t$ be a random process standing for the underlying price under a risk neutral probability. [ \forall t \in \mathbb{R}, S_t = e^{rt + X_t} ]
with $X_t$ a Lévy process with characteristic triplet $(\sigma, \nu, \gamma)$
Let’s note $ \forall t \in \mathbb{R}^+ $, $ C(t) = e^{ \int\limits_0^t r(s)ds } $,
$ \Leftrightarrow $ $ \frac{d C(t)}{C(t^-)} = r dt $ $ \Leftrightarrow $ $ C(t) = \int\limits_0^t r C(s^{-}) ds $
We have
[ \forall t \in \mathbb{R}, \tilde{S}t = \frac{S_t}{C_t} = e^{X_t} = A_t + M_t ]
with $ A_t $ and $ M_t $ defined in the previous decomposition formula.
Under the risk neutral probability, the actualized future price must be a martingale. We can write:
[ d\tilde{S}t = d( A_t + M_t ) = dA_t + dM_t ]
Therefore, we must have $ dA_t = 0 $ and then:
$ \gamma + \frac{\sigma^2}{2} + \displaystyle \int\limits{\mathbb{R}} [ e^{x} - 1 - x 1{|x| < 1}] \nu (dx) = 0 $
The dynamic of the actualized underlying is:
[ d\tilde{S}t = dM_t =S{t^-} , [ , \sigma d W_t + \int\limits_{\mathbb{R}} [ e^{x} - 1 ] \tilde{J}_X (dt \times dx) , ] ]
The dynamic is: [ \frac{dS_t}{S_t^-} = r dt + \sigma dW_t + \int\limits_{\mathbb{R}} (e^x - 1) \tilde{J}_X (dt \times dx) ]
with
- $ r, \sigma \in \mathbb{R}^2 $
- $ \tilde{J}_X (ds \times dx) = J_X (ds \times dx) - \nu(dx) ds $
- $ \nu $ the Lévy measure of $X$
- $ J_X $ the random Poisson measure on $\mathbb{R}^+$ with intensity $dt \times \nu $
Partial integro-differential equation
Let’s note $\forall t \in \mathbb{R}, , V(t,S_t)$ the price of a contingent claim.
To find the partial integro-differential equation, let’s notice that under the risk neutral probability the actualised future price must be a martingale.
Applying Itô formula, $\forall t \in \mathbb{R}$,
\begin{align*}
d( e^{-rt} V(t,S_t)) = & -r e^{-rt}V(t,S_t) dt + e^{-rt} \frac{\partial V(t,S_t)}{\partial t}dt + e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} dS_t \
& + e^{-rt}\frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} dt + e^{-rt} \Delta V(t,S_t) - e^{-rt} \frac{\partial V(t,S_t)}{\partial S_t}\Delta S_t
\end{align*}
With:
\begin{align*}
dS_t & = S_t^- \left[ r dt + \sigma dW_t + \int\limits_{\mathbb{R}} (e^x - 1) \tilde{J}_X (dt \times dx) \right] \
\Delta S_t & = S_{t^-}e^{\Delta X_t} - S_{t^-} = \int\limits_{\mathbb{R}} S_{t^-} (e^x - 1) J_X (dt \times dx) \
\Delta V(t,S_t) & = V(t,S_{t^-}e^{\Delta X_t} ) - V(t,S_{t^-}) = \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] J_X (dt \times dx)
\end{align*}
By replacing:
\begin{align*}
d( e^{-rt} V(t,S_t)) = & -r e^{-rt}V(t,S_t) dt + e^{-rt} \frac{\partial V(t,S_t)}{\partial t}dt + e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-[r dt + \sigma dW_t \
& + \int\limits_{\mathbb{R}} (e^x - 1) \tilde{J}_X (dt \times dx)] + e^{-rt}\frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} dt \
& + e^{-rt} \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] J_X (dx \times dt) \
& - e^{-rt} \frac{\partial V(t,S_t)}{\partial S_t}\int\limits_{\mathbb{R}} S_{t^-} (e^x - 1) J_X (dt \times dx) \
d( e^{-rt} V(t,S_t))= & -r e^{-rt}V(t,S_t) dt + e^{-rt} \frac{\partial V(t,S_t)}{\partial t}dt \
& + e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-r dt
- e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-\sigma dW_t \
& + e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-\int\limits_{\mathbb{R}} (e^x - 1) J_X (dt \times dx) \
& - e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-\int\limits_{\mathbb{R}} (e^x - 1) \nu (dt) dx \
& + e^{-rt}\frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} dt + e^{-rt} \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] J_X (dt \times dx) \
& - e^{-rt} \frac{\partial V(t,S_t)}{\partial S_t}\int\limits_{\mathbb{R}} S_{t^-} (e^x - 1) J_X (dt \times dx) \
d( e^{-rt} V(t,S_t)) = & -r e^{-rt}V(t,S_t) dt + e^{-rt} \frac{\partial V(t,S_t)}{\partial t}dt \
& + e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-r dt + e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-\sigma dW_t \
& - e^{-rt}\frac{\partial V(t,S_t)}{\partial S_t} S_t^-\int\limits_{\mathbb{R}} (e^x - 1) \nu (dt) dx + e^{-rt}\frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} dt \
& + e^{-rt} \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] \tilde{J}_X (dt \times dx) \
& + e^{-rt} \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] \nu (dx) dt \end{align*}
We can split the formula with a martingale part and a finite variation part. We have: \begin{align*} \forall t \in \mathbb{R}, d A_t = & e^{-rt} , [ , -r V(t,S_t) dt + \frac{\partial V(t,S_t)}{\partial t}dt + \frac{\partial V(t,S_t)}{\partial S_t} S_{t^-} r dt
- \frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} dt \
& + \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] \nu (dx) dt - \frac{\partial V(t,S_t)}{\partial S_t}\int\limits_{\mathbb{R}} S_{t^-} (e^x - 1) \nu (dx) dt , ] \
\forall \in \mathbb{R}, d M_t = & e^{-rt} , [ , \frac{\partial V(t,S_t)}{\partial S_t} S_{t^-} \sigma dW_t + \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] \tilde{J}_X (dt \times dx) , ] \end{align*}
with $ \forall t \in \mathbb{R} $, $A_t$ the finite variation part and $ \forall \in \mathbb{R} $, $M_t$ the martingale part.
We have to cancel the finite variation part. The partial integro-differential equation is therefore, $ \forall t \in \mathbb{R} $,
\begin{align*} 0 = & e^{-rt} , [ , -r V(t,S_t) dt + \frac{\partial V(t,S_t)}{\partial t}dt + \frac{\partial V(t,S_t)}{\partial S_t} S_{t^-} r dt
- \frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} dt \
& + \int\limits_{\mathbb{R}} [ V(t,S_{t^-}e^x ) - V(t,S_{t^-}) ] \nu (dx) dt - \frac{\partial V(t,S_t)}{\partial S_t}\int\limits_{\mathbb{R}} S_{t^-} (e^x - 1) \nu (dx) dt , ] \
r V(t,S_t) = & \frac{\partial V(t,S_t)}{\partial t} + \frac{\partial V(t,S_t)}{\partial S_t} S_{t^-} r + \frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} \
& + \int\limits_{\mathbb{R}} , [ , V(t,S_{t^-}e^x ) - V(t,S_{t^-}) - \frac{\partial V(t,S_t)}{\partial S_t} S_{t^-} (e^x - 1) , ] , \nu (dx) \
r V(t,S_t) = & \frac{\partial V(t,S_t)}{\partial t} + \frac{\partial V(t,S_t)}{\partial S_t} S_{t^-} , [ , r + \int\limits_{\mathbb{R}} , S_{t^-} (e^x - 1) , \nu (dx) , ] , \
& + \frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} + \int\limits_{\mathbb{R}} V(t,S_{t^-}e^x ) - V(t,S_{t^-}) , \nu (dx) \end{align*}
Remark:
If the Lévy measure is always equals to 0 then the PIDE is in fact the well known PDE applying to continuous Lévy processes.
For $ \frac{d S_t}{S_t} = r dt + \sigma d W_t $, we have the following valuation PDE:
[
\forall t \in \mathbb{R},
r V(t,S_t) = \displaystyle \frac{\partial V(t,S_t)}{\partial t} + \frac{\partial V(t,S_t)}{\partial S_t} S_t r
- \frac{\partial^2 V(t,S_t)}{\partial S_t^{,,2}} \frac{\sigma^2}{2} ]
Jump diffusion models
We decide to focus ourselves on a subset of jump diffusion models. We expose the advantage of introducing jumps in the underlyings dynamic. We find the dynamic and the risk neutral probability. The reader can expand/collapse for more information
Why Jump diffusion models ?
Empirically we observe the following characteristic for the underlying returns:
- They don't follow a log normal law. We observe heavy-tailed distribution and the kurtosis is not null
- They are not continuous
- We observe the volatility clustering phenomenon
Underlyings dynamic (for finite activity)
Let $W$ be a brownian motion and $J$ a composed Poisson process.
We note the filtration $ (\mathcal{F}t) = ( \sigma(W_s){s \le t} ) \lor ( \sigma(J_s)_{s \le t} ) $
with $ \lor $ defined by $ \mathcal{F}_1 \lor \mathcal{F}_2 $ is the smallest filtration including $ \mathcal{F}_1 \bigcup \mathcal{F}_2 $.
The dynamic in the jump model framework is split in two parts: a continuous diffusion part and a jump part.
the dynamic under the risk neutral probability is: [ \displaystyle \frac{d S_t}{S_{t^{-}}} =\underbrace{\mu (t^{-},S_{t^{-}}) dt + \sigma ({t^{-}},S_{t^{-}}) d W_t}_{continuous ; part} + \underbrace{d J_t}_{jump ; part} \text{with } J_t = \displaystyle \sum_{ i = 1}^{N_t} ( A_i - 1 ) ]
let’s note $ \displaystyle \frac{d S_t}{S_{t^{-}}} = d X_t$ . We can compute both parts:
- $ d X_t^c = \mu ({t^{-}},S_{t^{-}}) dt + \sigma ({t^-},S_{t^-}) d W_t $ so $ X_t^c - X_0^c = \displaystyle \int\limits_0^t \mu ({s^{-}},S_{s^{-}}) ds + \displaystyle \int\limits_0^t \sigma ({s^{-}},S_{s^{-}}) d W_s $
- $ d [X]_t^c = \sigma({t^{-}},S_{t^{-}})^2 d t $ so $ [X]_t^c = \displaystyle \int\limits_0^t \sigma ({s^{-}},S_{s^{-}})^2 ds $
- $ \displaystyle \prod_{ s \le t } ( 1 + \triangle X_s ) = \displaystyle \prod_{ i = 1 }^{N_t} A_i $
The underlying price is: [ S_t = \displaystyle S_0 \exp \left[ \int\limits_{0}^t ( \mu ({s^-},S_{s^-}) - \frac{\sigma ({s^-},S_{s^-})^2}{2} ) , \mathrm ds
- \int\limits_{0}^t \sigma ({s^-},S_{s^-}) , \mathrm d W_s \right] \displaystyle \prod_{i=1}^{N_t} A_i ]
Risk neutral probabilities
Let’s note $ \mu_a = \mathbb{E} [ A_1] = \mathbb{E} [ A_{N_t}]$, the mean of the jump size.
First of all, we have to prove that $ ( J_t - \mu_a \displaystyle \int\limits_0^t \lambda (s) ds )_{t} $ is a ($ \mathcal{F}_t $)-martingale.
Let’s note $ M(t) = J_t - \mu_a \displaystyle \int\limits_0^t \lambda (s) ds $.
We have $\mathbb{E} [ J_t ] = \mu_a \displaystyle \int\limits_0^t \lambda (s) ds $.
\begin{align*}
\mathbb{E} [ M(t) , | , \mathcal{F}_s ] & = \mathbb{E} [ J_t - \mu_a \displaystyle \int\limits_0^t \lambda (s) ds , | , \mathcal{F}_s ]
= \mathbb{E} [ J_t - J_s - \mu_a \displaystyle \int\limits_s^t \lambda (u) du , | , \mathcal{F}_s ] + J_s - \mu_a \displaystyle \int\limits_0^s \lambda (u) du \
& = \underbrace{\mathbb{E} [ \displaystyle \sum_{k= 1+N_s}^{N_t} A_i , | , \mathcal{F}_s ]
- \mu_a \displaystyle \int\limits_s^t \lambda (u) du }_{=0} + J_s - \mu_a \displaystyle \int\limits_0^s \lambda (u) du = J_s - \mu_a \displaystyle \int\limits_0^s \lambda (u) du = M(s) \end{align*}
Because $ \mathbb{E} [ M(t) , | , \mathcal{F}s ] = J_s - \mu_a \displaystyle \int\limits_0^s \lambda (u) du = M(s) $ with $ \frac{d S_t}{S{t^{-}}} = \mu (t^{-},S_{t^{-}}) dt + \sigma ({t^{-}},S_{t^{-}}) d W_t + d J_t $.
The discount factor is noted $D_t$ and is equal to: $D_t = e^{ - \int\limits_{0}^t r(s) , \mathrm ds} $
\begin{align*}
d ( D_t S_t ) & = - r(t) D_t S_t dt + D_t d S_t \
D_t S_t & = \displaystyle \int\limits_0^t D_{s^-} S_{{s^-}} [ ( \mu (s^{-},S_{s^{-}})- r(s) ) ds + \sigma ({s^{-}},S_{S^{-}}) d W_s + d J_s ] + D_0 S_0 \
D_t S_t & = \displaystyle \int\limits_0^t D_{s^-} S_{{s^-}} [ \mu (s^{-},S_{s^{-}}) + \lambda(s^-) (\mu_a - 1 ) - r(s^-) ] ds \
& + \displaystyle \int\limits_0^t D_{s^-} S_{{s^-}} \sigma ({s^{-}},S_{s^{-}}) d W_s \displaystyle + \int\limits_0^t D_{s^-} S_{{s^-}} d M_s + D_0 S_0 \
\end{align*}
Therefore
\begin{align*}
& D_t S_t - \displaystyle \int\limits_0^t D_{s^-} S_{{s^-}} \sigma ({s^{-}},S_{s^{-}}) d W_s - \displaystyle \int\limits_0^t D_{s^-} S_{{s^-}} d M_s \
& = \displaystyle \int\limits_0^t D_{s^-} S_{{s^-}} [ \mu (s^{-},S_{s^{-}}) + \lambda(s^-) (\mu_a - 1 ) - r(s^-) ] ds + D_0 S_0
\end{align*}
On the left side is a linear combination of martingale (an integral again a martingale is still a martingale).
Therefore, the right side is also a martingale. We have:
[ \int\limits_{0}^{\cdot} ( \mu ({u^-},S_{u^-}) - r_{u^-} + \lambda_{u^-} [ \mu_a - 1] ; ), \mathrm du ] which is a martingale so:
[ \forall t \in \mathbb{R}^+ ,; \mu (t,S_t) - r_t + \lambda_{t} [ \mu_a - 1] = 0
\Leftrightarrow ; \forall t ; \mu (t,S_t) = r_t - \lambda_{t} [ \mu_a - 1] ]
Under the risk neutral probability, the underlying price is: \[ S_t = S_0 \displaystyle \exp \left[ \int\limits_{0}^t \left( r_{u^-} - \lambda_{u^-} [ \mu_a - 1] - \frac{\sigma ({u^-},S_{u^-})^2}{2} \right) \, \mathrm du + \int\limits_{0}^t \sigma ({u^-},S_{u^-}) \, \mathrm d W_u \right] \displaystyle \prod_{i=1}^{N_t} A_i \]
Merton jump diffusion model
A model having this features is the Merton model. We expose the dynamic of the underlyings and the european call price formula. We also investigate the calibration procedure in this model.
The dynamic in this model is the following one: \[ \frac{d S_t}{S_{t^{-}}} = ( r_{t^-} - \lambda_{t^-} [ \mu_a - 1] ) dt + \sigma_{t^-} d W_t + d J_t \]
with
- the interest rate $r$ and the volatility $\sigma$ are supposed to be deterministic functions
- $ \forall \mu_z, \sigma_z \in \mathbb{R}^2 A_i = e^{\mu_z + \sigma_z Zi} $
- $ \forall n, (Z_1, ... ,Z_n ) \sim \mathcal{N}(0, I_n)$
- $ \forall i \in \mathbb{N}^*, \forall t \in \mathbb{R}^+, A_i \perp\!\!\!\perp N_t $
- $ \mu_a = exp( \mu_z + \frac{\sigma_z^2}{2} )$
The underlying price is
\begin{align*} S_t & = \displaystyle S_0 \exp \left( \int\limits_{0}^t ( r_{s^-} - \lambda_{s^-} [ \mu_a - 1] - \frac{\sigma_{s^-}^2}{2} ) \, \mathrm ds + \int\limits_{0}^t \sigma_{s^-} \, \mathrm d W_s \right) \displaystyle \prod_{i=1}^{N_t} A_i \\ & = S_0 \exp \left( \, \int\limits_{0}^t ( r_{s^-} - \lambda_{s^-} [ \mu_a - 1] - \frac{\sigma_{s^-}^2}{2} ) \, \mathrm ds + \int\limits_{0}^t \sigma_{s^-} \, \mathrm d W_s + \displaystyle \sum_{i=1}^{N_t} [ \mu_z + \sigma_z \; Z_i ] \, \right) \end{align*}
European call price
We expose in this section three different methods to compute a call price in the Merton model:
- Monte-Carlo
- PIDE
- Series expansion
Let’s compute the call price under the risk neutral probability previously exposed. A same computation can be apply for Put price.
The steps are the followings:
- Apply the law of iterated expectations using the Poisson process conditioning
- Compute the new log normal parameters
- Compute the expected value of a Black-Scholes call as a function of the Poisson law
Let’s compute the call price: [ \mathbb{E} \left[ e^{ - \int\limits_{s}^t r_u \mathrm du } ; ( S_t - K )_{+} , | , \mathcal{F}_s \right] = \mathbb{E} \left[ ; \mathbb{E} [ ; e^{ - \int\limits_{s}^t r_u \mathrm du } ; ( S_t - K )_{+} | N_t =n ; ] ; , | , \mathcal{F}_s \right] ]
Let’s identify the law of $ S_t $ conditional to the event {$ N_t = n $}: [ S_t | N_t , \mathcal{F}s \overset{\mathcal{L}}{=} S_s \exp \left( ; \int\limits{s}^t ( r_{u^-} - \lambda_{u^-} [ \mu_a - 1]
- \frac{\sigma_{u^-}^2}{2} ) , \mathrm du + \int\limits_{s}^t \sigma_{u^-} , \mathrm d W_u + n \mu_z + \sqrt{n} \sigma_z ; Z_1 ; \right) ]
Moreover, we know that $ \int\limits_{s}^t \sigma_u , \mathrm d W_u \sim N ( 0 , \int\limits_{s}^t \sigma_u^2 , \mathrm du ) $.
Let’s write the integral against the brownian motion using law equalities:
\begin{align*}
\int\limits_{s}^t \sigma_{u^-} , \mathrm d W_u + \sqrt{n} \sigma_z L &\overset{\mathcal{L}}{=}
\sqrt{ ( \int\limits_{s}^t \sigma_{u^-}^2 , \mathrm du + n \sigma_z^2 } ) ; L
\overset{\mathcal{L}}{=} \sqrt{( \int\limits_{s}^t \sigma_{u^-}^2 , \mathrm du + n \sigma_z^2 )}
; \frac{( W_t - W_s )}{ \sqrt{t-s} }\
&\overset{\mathcal{L}}{=} \sqrt{ \frac{1}{ t - s } \left( \int\limits_{s}^t \sigma_{u^-}^2 , \mathrm du + n \sigma_z^2 \right) } ( W_t - W_s )
\end{align*}
with $L$ which follow a standard normal distribution. We have in law: [ S_t | N_t , \mathcal{F}s \overset{\mathcal{L}}{=} S_s \exp \left( ; \int\limits{s}^t ( r_{u^-}
- \lambda_{u^-} [ \mu_a - 1] - \frac{\sigma_{u^-}^2}{2} ) , \mathrm du + n \mu_z
- \sqrt{ \frac{\int\limits_{s}^t \sigma_{u^-}^2 , \mathrm du }{ t - s } + \frac{n \sigma_z^2}{ t - s } } ; ( W_t - W_s ) ; \right) ]
\begin{align*}
S_t | N_t , \mathcal{F}_s \overset{\mathcal{L}}{=} S_s & \exp \left( n \mu_z - \int\limits_{s}^t \lambda_{u^-} du [ \mu_a - 1] + \frac{n \sigma_z^2}{ 2 } \right) \
& \exp \left( ; \int\limits_{s}^t r_{u^-} - \frac{\sigma_{u^-}^2}{2} , \mathrm du - \frac{n \sigma_z^2}{ 2 }
- \sqrt{ \frac{\int\limits_{s}^t \sigma_{u^-}^2 , \mathrm du }{ t - s } + \frac{n \sigma_z^2}{ t - s } } ; ( W_t - W_s ) ; \right) \end{align*}
We can therefore note $ \bar S_s (n) $ the new $ S_s $ and $ \bar \sigma (n) $ the new $ \sigma_t $:
\begin{align*}
\bar S_s (n) & = S_s \exp \left( \int\limits_{s}^t \lambda_{u^-} du [1 -\mu_a] + n \mu_z + \frac{n \sigma_z^2}{ 2 } \right) \
\bar \sigma (n) & = \sqrt{ \frac{n \sigma_z^2 }{t-s} + \frac{ \int\limits_{s}^t \sigma_{s^-}^2 ds}{t-s} }
\end{align*}
We have: [ S_t | N_t , \mathcal{F}s \overset{\mathcal{L}}{=} \bar S_s (N_t) \exp \left( ; \int\limits{s}^t r_{u^-} , \mathrm du
- \frac{ \bar \sigma (N_t)^2}{2} (t-s) + \bar \sigma (N_t) ; (W_t - W_s) ; \right) ]
Let’s back to the initial conditional expectation: [ \mathbb{E} \left[ ; \mathbb{E} \left[ e^{- \int\limits_{s}^t r_u \mathrm du } ; ( S_t - K )_{+} | N_t =n ; \right] ; | \mathcal{F}_s \right] = \mathbb{E} \left[ C_{BS}( \bar{S_s}(k),K,r,t,\bar{\sigma}(k)) | \mathcal{F}_s \right] ]
Under the Black-Scholes model, we recall the european call closed form:
\begin{align*}
C_{BS} & ( S_s, K, r, T,\sigma ) = S_s N(d1) - K exp(-r T) N(d2) \
d1 & = \frac{1}{\sigma \sqrt{T}} [ ln( \frac{S_s}{K} ) + ( r + \frac{\sigma^2}{2} ) T ] \
d2 & = d1 - \sigma \sqrt{T}
\end{align*}
We therefore have to compute the $ C_{BS} $ with the new parameters previously found.
The Merton call price is given by: \[ Call (s,T,S,K) = \displaystyle \sum_{k = 0}^{\infty} \mathbb{P} ( N_t = k ) \times C_{BS}( \bar{S_s}(N_t),K,r,t,\bar{\sigma}(N_t) ) \]
Error control in call pricing
We have to find a stopping criteria for the previous series expansion, we want to identify $ k_{opt}$ such that \begin{align*} Err (k_{opt}) = & |\frac{1}{S_0} ( \displaystyle \sum_{k = 0}^{\infty} f(k) - \displaystyle \sum_{k = 0}^{k_{opt}} f(k) ) | < \epsilon \\ f(k) = & \mathbb{P} ( N_t = k ) \times T(k) \\ T(k) = & C_{BS}( \bar{S_s}(k),K,r,t,\bar{\sigma}(k)) \end{align*}
Let’s suppose $ \lambda $ constant for the purpose of clarity
\begin{align*}
S_0 \times Err(k)
& = | \displaystyle \sum_{k = 0}^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } T(k) - \displaystyle \sum_{k = 0}^{k_{opt}} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } T(k) |
= | \displaystyle \sum_{k = k_{opt}+1 }^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } T(k)| \
& = | \displaystyle \sum_{k = k_{opt}+1 }^{\infty} \mathbb{P} ( N_t = k ) T(k)|
\end{align*}
Using the non arbitrary conditions, we can write $ T(k) \le \bar{S_0} $.
Moreover, all the terms of the sum are positive, so:
[
S_0 \times Err(k) \le \displaystyle \sum_{k = k_{opt}+1 }^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } \bar{S}_0
= {e^{-\lambda t}} \displaystyle \sum_{k = k_{opt}+1 }^{\infty} {\frac{(\lambda t)^k}{k!} } S_0 \exp ( \lambda t [1 -\mu_a] + k \mu_z + \frac{k \sigma_z^2}{ 2 } )
]
[
= {e^{ - \lambda t \mu_a } } \displaystyle \sum_{k = k_{opt}+1 }^{\infty} {\frac{(\lambda t)^k}{k!} } S_0 \exp ( k \mu_z + \frac{k \sigma_z^2}{ 2 } )
= S_0 {e^{- \lambda t \mu_a } } \displaystyle \sum_{k = k_{opt}+1 }^{\infty} {\frac{(\lambda t)^k}{k!} } \mu_a^k
]
Let’s note $ y = \lambda t \mu_a $, [ S_0 \times Err ( k_{opt} ) \le S_0 {e^{-y} } \displaystyle \sum_{k = k_{opt}+1 }^{\infty} {\frac{y^k}{k!} } = S_0 {e^{-y} } [ e^{y} - \displaystyle \sum_{k = 0 }^{k_{opt}} {\frac{y^k}{k!} } ] ] [ Err ( k_{opt} ) \le {e^{-y} } [ e^{y} - \displaystyle \sum_{k = 0 }^{k_{opt}} {\frac{y^k}{k!} } ] ]
We simply have to test if $ e^{y} - \displaystyle \sum_{k = 0}^{k_{opt}}{\frac{(y)^k}{k!} } $ is lower than a chosen tolerance.
Numerically, this sum can be directly computed. We have to accumulate the term inside the price computation.
Greeks computation
Greeks can be computed using a closed form by applying the chain rule. The reader can expand/collapse for more details on greeks.
\begin{align*}
\delta = \frac{\partial Call }{\partial S } = &
\displaystyle \sum_{k = 0}^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } \times \delta^{BS}(k)
\times \exp \left( \int\limits_{0}^t \lambda_s ds [1 -\mu_a] + k \mu_z + \frac{k \sigma_z^2}{ 2 } \right) \
\gamma = \frac{\partial^2 Call }{\partial S^2 } = &
\displaystyle \sum_{k = 0}^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } \times \gamma^{BS}(k)
\times \exp \left( 2 [ \int\limits_{0}^t \lambda_s ds [1 -\mu_a] + k \mu_z + \frac{k \sigma_z^2}{ 2 } ] \right) \
vega = \frac{\partial Call }{\partial \sigma } = &
\displaystyle \sum_{k = 0}^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } \times vega^{BS}(k) \times \frac{\sigma_t \sqrt{t}} {n \sigma_z^2 + \int\limits_{0}^t \sigma_t^2 } \
\frac{\partial Call }{\partial K } & = \displaystyle \sum_{k = 0}^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } \times \frac{\partial C_{BS}}{\partial K }(k) \
\frac{\partial^2 Call }{\partial K^2 } & = \displaystyle \sum_{k = 0}^{\infty} {e^{-\lambda t}} {\frac{(\lambda t)^k}{k!} } \times \frac{\partial^2 C_{BS} }{\partial K^2 }(k)
\end{align*}
Generic calibration procedure
Let introduce the classical calibration procedure. \[ \underset{p \in \mathcal{P}}{\arg} \min { \displaystyle \sum_{i \in I} w_i { ( \sigma_i^{mod}(p) - \sigma_i^{mkt} )^2 } } \] with
- $ \mathcal{P} $ set of model parameters
- $I$ set of indexes related to the quoted options
- $ {(w_i})_{i \in I} $ a weight family
- $ \sigma_i^{mkt} $ implied volatility for the $i^{th}$ option
- $ \sigma_i^{mod} (p) $ equivalent Black-Scholes volatility using $p$ parameters
- $V_i^{BS}$: BS price for the $i^{th}$ option.
- $ VegaBS_i = \displaystyle \frac{ \partial {V^{BS}} }{ \partial \sigma } $
By definition,
\begin{align*}
& V_i^{mod} = V_i^{BS} (\sigma_i^{mod}(p)) \
& V_i^{mkt} = V_i^{BS} (\sigma_i^{mkt})
\end{align*}
Using Taylor series, we have: [ V_i^{BS} (\sigma_i^{mod}(p)) = V_i^{BS} (\sigma_i^{mkt}) + ( \sigma_i^{mod}(p) - \sigma_i^{mkt} ) \displaystyle \frac{\partial V_i^{BS} }{\partial \sigma } (\sigma_i^{mkt})
- O ( \sigma_i^{mod}(p) - \sigma_i^{mkt} )^2 ]
\begin{align*} \sigma_i^{mod}(p) - \sigma_i^{mkt} & = \displaystyle \frac{ V_i^{BS} (\sigma_i^{mod}(p)) - V_i^{BS} (\sigma_i^{mkt}) }{ \frac{\partial V_i^{BS} }{\partial \sigma } (\sigma_i^{mkt}) }
- O ( \sigma_i^{mod}(p) - \sigma_i^{mkt} )^2 \
& = \displaystyle \frac{ V_i^{BS} (\sigma_i^{mod})(p) - V_i^{BS} (\sigma_i^{mkt}) }{ VegaBS_i (\sigma_i^{mkt}) } + O ( \sigma_i^{mod}(p) - \sigma_i^{mkt} )^2 \end{align*}
[ \underset{p \in \mathcal{P}}{\arg} \min \displaystyle \sum_{i \in I} w_i \left[ { \frac{ V^{BS} (\sigma_i^{mod}(p)) - V^{BS} (\sigma_i^{mkt}) }{ VegaBS_i (\sigma_i^{mkt}) } } \right]^2 ]
Parameters impact
To expose the parameters influence, we expose the implied volatility surface in function of the model parameters. Don’t hesitate to expand this section
Let’s have the following parameters:
- s0 = 100 and r = 0.02
- lambda = 0.2
- sigma = 0.3
- mu_z = -0.3
- sigma_z = 0.1
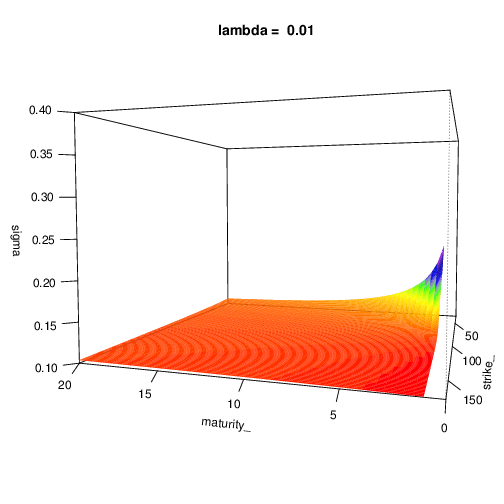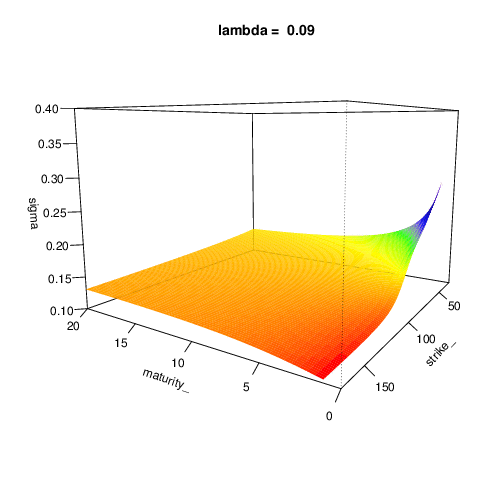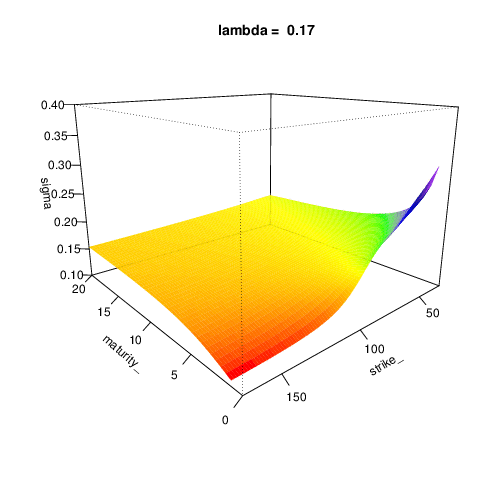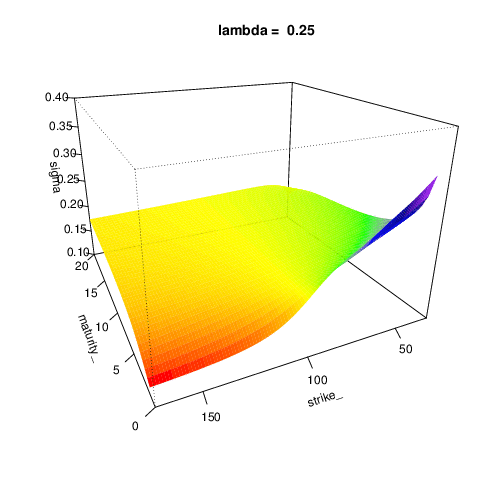
Bates Model
This model merges the benefits of Merton and Heston models.
The underlying dynamic is based on the Black-Scholes one with two additional features:
- Jump part: control the smile for short term smile (< 1 an)
- Stochastic volatility part, follow a Cox Ingersoll Ross (CIR) process: control the smile for higher maturities (> 1 an)
General dynamic
Let $W^s$ and $W^v$ two brownian motions with correlation $\rho \in \mathopen{[}-1,1\mathclose{]}$.
Let $J$ be a composed Poisson process.
Let have the filtration $ (\mathcal{F}t) = ( \sigma(W_u^s){u \le t} ) \lor ( \sigma(W_u^v){u \le t} ) \lor ( \sigma(J_u){u \le t} ) $
The underlying dynamic is the following one:
\begin{align*}
\frac{d S_t}{S_{t^{-}}} & = ( r_t + \lambda ( 1 - \mu_a) ) dt + \sqrt{V_{t^{-}}} d W_t^s+ d J_t \
dV_{t} & = \xi (\eta - V_{t}) dt + \theta \sqrt{V_{t}} d W_t^v
\end{align*}
with
- $ J_t = \displaystyle \sum_{ i = 1}^{N_t} ( A_i - 1 ) $ with $ \forall i \in \mathbb{N}^*, \forall t \in \mathbb{R}^+, A_i \perp\!\!\!\perp N_t $ and $ A_i $ iid
- $ \forall n, (Z_1, ... ,Z_n ) \sim \mathcal{N}(0, I_n)$ $A_i = e^{\mu_z + \sigma_z Z_i } $ with $ \mu_z \in \mathbb{R}$ and $ \sigma_z \in \mathbb{R}^+$
- $( \xi $, $ \eta $ , $ \theta )\in {\mathbb{R}^3}^+ $
- $ \mu_a = e^{\mu_z + \frac{\sigma_z^2}{2}} $
European call price
We expose in this section three different methods to compute a call price in the Bates model:
- Monte-Carlo
- PIDE
- Fourier transform (available for all models with a known characteristic function for the underlying)
For Monte-Carlo and PIDE methods, we refer the reader to the book of R. Cont and P. Tankov: “Financial Modelling with Jump Processes”.
We develop the Fourier transform in the following section.
Fourier transform method
We first recall the general Fourier transform pricing then apply it to the Bates model case.
The reader can expand/collapse for more details on Call/Put valuation using Fourier transform method
Let introduce some notations:
- $ Call(t, S, K, T) $ the price of an european call in the Bates model with maturity $T$ and strike $K$
- $ \forall t \in \mathbb{R}^{+*}, S_t = C(t) e^{X_t} $ the underlying price with $ \forall t \in \mathbb{R}^*$, $ X_t $ a random process with known moment-generating function noted $ \chi $
The first step is to rewrite the european call price as follow: \begin{equation*} Call(0, S, K, t) = \frac{1}{C(t)} \mathbb{E} [ (S_t - K)_{+} | F_{0}] = S_0 \mathbb{E} [ (e^{X_t} - \frac{K}{S_0 C(t)} )_{+} | F_{0}] = S_0 \mathbb{E} [ (e^{X_t} - e{^k})_{+} | F_{0}] \end{equation*}
with $ k = log ( \frac{K}{S_0 C(t)} ) $.
Remark that $ \mathbb{E} [ (e^{X_t} - e{^k}){+} | F{0}] = \mathbb{E} [ (e^{X_t} - e^{k} ( e^{X_t - k} \land 1) ) | F_{0}]$
Let’s develope the conditional expectation:
[
\mathbb{E} [ (e^{X_t} - e^{k} \left( e^{X_t - k} \land 1) \right) | F_{0}]
= \displaystyle \int\limits_{-\infty}^{\infty} e^{x} f(x) dx - e^{(-\alpha + 1) k} \displaystyle \int\limits_{-\infty}^{\infty} ( 1 \land e^{- (k - x) } ) e^{ \alpha (k - x)} e^{ \alpha x} f(x) dx
]
with $ f(x) $ the density function of $X_t$ and $ \alpha \in \mathopen{[}0,1\mathclose{]}$
We have the following result:
[
\mathbb{E} [ (e^{X_t} - e{^k}){+} | F{0}] = \chi (1) - e^{(-\alpha + 1)k} \displaystyle \int\limits_{-\infty}^{\infty} ( 1 \land e^{- (k - x) } ) e^{ \alpha (k - x)} e^{ \alpha x} f(x) dx
]
Let’s note: $ g(x) = ( 1 \land e^{- x} ) e^{ \alpha x} $ and $ h(x) = e^{ \alpha x} f(x) $
Using the property:
$ g * h = TF^{-1} ( TF (g * h) ) = TF^{-1} ( TF (g) TF (h) )$
We can compute the two followings Fourier transform:
\begin{align*}
TF (g) (u) & = \int\limits_{-\infty}^{\infty} e^{i u x} ( 1 \land e^{- x} ) e^{ \alpha x} \
& = \int\limits_{-\infty}^{0} e^{i u x + \alpha x} dx + \int\limits_{0}^{\infty} e^{i u x + x (\alpha-1) } dx \
& = \displaystyle \frac{1}{i u + \alpha} - \frac{1}{i u + \alpha -1} = \frac{-1}{(i u + \alpha) (i u + \alpha -1)} \
TF (h) (u) & = \int\limits_{-\infty}^{\infty} e^{i u x} e^{ \alpha x} f(x) dx = \chi (\alpha + i u)
\end{align*}
Therefore, we have:
$ g * h = \frac{- 1}{2 \pi} \displaystyle \int\limits_{-\infty}^{\infty} \frac{e^{-k i u }}{(i u + \alpha) (i u + \alpha -1)} \chi (\alpha + i u) du $
The call price is finally:
[ Call(0, S, K, t) = S_0 \chi(1) + S_0 \displaystyle \frac{ e^{k (-\alpha + 1)}}{2 \pi} \displaystyle
\int\limits_{-\infty}^{\infty} \frac{e^{-k i u }}{(i u + \alpha) (i u + \alpha -1)} \chi (\alpha + i u) du ]
Because the function are Hermitian $ \overline{\chi (\alpha + iu)} = \chi (\alpha - iu) $, we have the property for a function $H$: $\forall x \in \mathbb{C}$, $ \overline{H(x)} = H(-x) $
Let’s rewrite the integral term:
$ \displaystyle \int\limits_{-\infty}^{+\infty} H (x) dx = \int\limits_{-\infty}^{0} H (x) dx + \int\limits_{0}^{+\infty} H (x) dx
= \displaystyle \overline{\int\limits_{0}^{+\infty} H (x) dx} + \int\limits_{0}^{+\infty} H (x) dx
= 2 Re ( \int\limits_{0}^{+\infty} H (x) dx ) $
We finally have: $ \displaystyle \int\limits_{-\infty}^{\infty} H (x) dx = 2 Re \int\limits_{0}^{\infty} H (x) dx $.
The price at 0 of an european call on S with maturity t and strike K is:
\begin{align*}
Call(0, S, K, t) = & S_0 \chi(1) + S_0 \frac{e^{k(-\alpha + 1)}}{\pi} \displaystyle \int\limits_{0}^{\infty}
Re \left( \frac{e^{-k i u}}{(i u + \alpha) (i u + \alpha -1)} \chi (\alpha + i u) \right) du \
= & S_0 \chi(1) + \displaystyle \left({\frac{K}{C(t)}}\right)^{(-\alpha + 1)} \frac{S_0^{\alpha}}{\pi} \displaystyle
\int\limits_{0}^{\infty} Re \left( \frac{e^{-k i u}}{(i u + \alpha) (i u + \alpha -1)} \chi (\alpha + i u) \right) du
\end{align*}
Application in the Bates model
The reader can expand/collapse for more details on Call valuation in Bates model using Fourier transform method
To increase the integral convergence, we add and remove the call price in another model, for instance in the Merton model noted $C_{M}$: [ Call(0, S, K, t) = C_{M}(0, S, K, t) + C(t)^{-1} \mathbb{E} [ (S_t - K)_{+} | F_{0}] - C_{M}(0, S, K, t) ]
Simply applying the previously found general formula, we have for $Call(0, S, K, t) $:
\begin{align*}
& C_{M}(0, S, K, t) \
& + S_0 \chi_{Bates}(1) + \left({\frac{K}{C(t)}}\right)^{(-\alpha + 1)} \frac{S_0^{\alpha} }{\pi} \displaystyle \int\limits_{0}^{\infty}
Re \left( \frac{e^{-k i u}}{(i u + \alpha) (i u + \alpha -1)} \chi_{Bates} (\alpha + i u) \right) du \
& - S_0 \chi_{m}(1) - \left({\frac{K}{C(t)}}\right)^{(-\alpha + 1)} \frac{S_0^{\alpha} }{\pi} \displaystyle
\int\limits_{0}^{\infty} Re \left( \frac{e^{-k i u}}{(i u + \alpha) (i u + \alpha -1)} \chi_{m} (\alpha + i u) \right) du \
= & C_{M}(0, S, K, t) \
& + \left({\frac{K}{C(t)}}\right)^{(-\alpha + 1)} \frac{S_0^{\alpha} }{\pi} \displaystyle \int\limits_{0}^{\infty} Re \left[ \frac{e^{-k i u}}{(i u + \alpha) (i u + \alpha -1)}
( \chi_{Bates} (\alpha + i u) - \chi_{m}(\alpha + i u) ) \right] du
\end{align*}
The first term is computed using the series expansion found in the section dedicated to the Merton model.
Expression of $\chi_{Bates}(u)$ and $\chi_{m}(u)$ $\forall u \in \mathbb{C}$
Computation of $\chi_{m}(u)$, $\forall u \in \mathbb{C}$
\begin{align*}
\forall u \in \mathbb{C}, \chi_m(u) & = \chi_m^d(u) \times \chi_m^c(u) \
\forall u \in \mathbb{C}, \chi_m^c(u) & = \chi_m^c(u) = \chi_{BS}(u) = e^{ - \frac{\sigma^2 t}{2}(u-u^2)} \
\forall u \in \mathbb{C}, \chi_{m}^d(u) & = \mathbb{E} [ e^{J_t} ] = e^{ \lambda t ( \chi_a(u) - 1 )} \
& = \displaystyle e^{ \lambda t \left( e^{u ( \mu_z + \frac{u \sigma_z^2}{2} )} - 1 \right)}
\end{align*}
With $\chi_a$ the Moment-Generating function of the random variable $A_i$.
We note $\forall u \in \mathbb{C}$, $ \displaystyle \chi_{m}^d(u) = \chi_{Jump}(u) $
Computation of $\chi_{Bates}(u)$, $\forall u \in \mathbb{C}$
\begin{align*}
\forall u \in \mathbb{C}, \chi_{Bates}(u) & = \chi_{Bates}^c(u) \times \chi_{Bates}^d(u) \
\forall u \in \mathbb{C},\chi_{Bates}^d(u) & = \chi_{Jump}(u) = \mathbb{E} [ e^{J_t} ] = exp\left(\lambda T( e^{u \mu_z + u^2 \frac{\sigma_z^2 }{2} } - 1)\right) \
\forall u \in \mathbb{C}, \chi_{Bates}^c(u) & = \chi_{Heston}(u)
\end{align*}
First of all, let’s note $ X = log(S) $.
Applying Itô formula to $ log(S) $, we have:
$ dX_t = (r_t + \lambda(1 - mu_a) - \frac{1}{2}V_t )dt + \sqrt{V_t} dW_t^s $
Let’s note $ \forall t \in \mathbb{R}^{+} $ $ M_t = f(X_t^c, V_t, t ) $ with
$ \forall (x,v,t) \in (\mathbb{R}^{+})^3 $ $ f(x, v, t ) = \mathbb{E} [ e^{u X_t^c} |X_t^c = x , V_t = v ] $
For the sake of clarity, let’s introduce $ f = f(X_t^c, V_t, t) $ and let’s apply the Itô formula for continuous processes to $ M_t $.
[
d M_t = \displaystyle \frac{\partial f }{\partial x } d X_t^c + \frac{\partial f }{\partial v } d V_t + \frac{\partial f }{\partial t } d t
- \frac{1}{2} \left[ \frac{\partial^2 f }{\partial x^2 } d[ X^c ]_t + \frac{\partial^2 f }{\partial v^2 } d[ V ]_t
- 2 \frac{\partial^2 f }{\partial x \partial v } d[ X^c , V ]_t \right]
]
Let’s compute each terms:
\begin{align*}
d X_t^c & = \displaystyle (r_t + \lambda (1 - \mu_A) - \frac{V_t}{2}) dt + \sqrt{V_t} d W_t^s \
d V_t & = \xi (\eta - V_{t}) dt + \theta \sqrt{V_{t}} d W_t^v \
d[ X^c ]_t & = V_t dt \
d[ V ]_t & = \theta^2 V_t dt \
d[ X^c , V ]_t & = \rho \theta V_t dt
\end{align*}
Substituting, we have:
\begin{align*} d M_t = & \displaystyle \frac{\partial f }{\partial x } ( (r_t + \lambda (1 - \mu_A) - \frac{V_t}{2}) dt + \sqrt{V_t} d W_t^s )
- \frac{\partial f }{\partial v } ( \xi (\eta - V_{t}) dt + \theta \sqrt{V_{t}} d W_t^v ) + \frac{\partial f }{\partial t } d t \
& \displaystyle + \frac{1}{2} [ \frac{\partial^2 f }{\partial x^2 } V_t + \frac{\partial^2 f }{\partial v^2 } \theta^2 V_t - 2 \frac{\partial^2 f }{\partial x \partial v } \rho \theta V_t ] dt \
= & [ \displaystyle \frac{\partial f }{\partial x } (r_t + \lambda (1 - \mu_A) - \frac{V_t}{2}) + \frac{\partial f }{\partial v } \xi (\eta - V_{t}) + \frac{\partial f }{\partial t } \
& + \frac{1}{2}\frac{\partial^2 f }{\partial x^2 } V_t + \frac{1}{2}\frac{\partial^2 f }{\partial v^2 } \theta^2 V_t + \frac{\partial^2 f }{\partial x \partial v } \rho \theta V_t ] dt + \displaystyle \theta \sqrt{V_{t}} d W_t^v + \sqrt{V_{t}} d W_t^s \end{align*}
Moreover, we know that $f(X_{\cdot}^c, V_{\cdot}, \cdot)$ has to be a martingale. The drift must be equals to zero because $f(X_{\cdot}^c, V_{\cdot}, \cdot)$ is continue. [ \displaystyle \frac{\partial f }{\partial x } (r_t + \lambda (1 - \mu_A) - \frac{V_t}{2})
- \frac{\partial f }{\partial v } \xi (\eta - V_{t}) + \frac{\partial f }{\partial t }
- \frac{1}{2}\frac{\partial^2 f }{\partial x^2 } V_t + \frac{1}{2}\frac{\partial^2 f }{\partial v^2 } \theta^2 V_t
- \frac{\partial^2 f }{\partial x \partial v} \rho \theta V_t = 0 ] with the terminal condition $ f(x,v,t) = e^{ux} $
We suppose the solution can be written as follow: $ f(x, v, t) = e^{ A(T-t) + v B(T-t) + u x } $ with initial condition $ A(0) = 0 $ and $ B(0) = 0 $.
We have:
\begin{align*}
\displaystyle \frac{\partial f }{\partial x } & = u f \
\frac{\partial f }{\partial v } & = B(T-t) f \
\frac{\partial f }{\partial t } & = - \frac{\partial A }{\partial t }(T-t) + -V_t \frac{\partial B }{\partial t }(T-t) \
\frac{\partial^2 f }{\partial x^2 } & = u^2 f \
\displaystyle \frac{\partial^2 f }{\partial v^2 } & = B(T-t)^2 f \
\frac{\partial^2 f }{\partial x \partial v } & = - u B(T-t) f
\end{align*}
The equation can be written by substituting: \begin{align*} & \displaystyle u f (r_t + \lambda (1 - \mu_A) - \frac{V_t}{2}) + B(t) f \xi (\eta - V_{t})
- (\frac{\partial A }{\partial t }(t) + V_t \frac{\partial B }{\partial t }(t) ) \
& + \frac{1}{2}u^2 f V_t + \frac{1}{2}B(t)^2 f \theta^2 V_t - u B(t) f \rho \theta V_t = 0 \end{align*}
\begin{align*}
& \displaystyle u(r_t + \lambda (1 - \mu_A)) + B(t)\xi \eta - \frac{\partial A }{\partial t }(t) \
& + \left[ - \frac{\partial B }{\partial t }(t)
- B(t)\xi + \frac{1}{2}u^2 + \frac{1}{2}B(t)^2 \theta^2 - u B(t) \rho \theta - \frac{u}{2} \right] V_t = 0 \end{align*}
The two solutions of our problem are:
\begin{align*}
\displaystyle \frac{\partial A }{\partial t }(t) & = B(t) \xi \eta + u (r_t + \lambda (1 - \mu_A)) \
\displaystyle \frac{\partial B }{\partial t }(t) & = \frac{1}{2}\theta^2 B(t)^2 - \xi B(t) - \rho \theta u B(t) + \frac{1}{2}u^2 - \frac{1}{2}u
= \frac{1}{2}\theta^2 B(t)^2 - ( \rho \theta u + \xi ) B(t) - \frac{u}{2}( 1 - u )
\end{align*}
The first one is an integral computation. The second one is a Riccati equation.
The solutions of our two equations can be written as follow:
\begin{align*}
\displaystyle A(t) & = u \left( \frac{1}{log ( C(t))} + t \lambda ( 1 - \mu_A) \right) +
\frac{\xi \eta t (\xi + \rho \theta u)}{\theta^2} - \frac{2 \xi \eta}{\theta^2} log \left( cosh ( \frac{\gamma t}{2} ) - \frac{\xi + \rho \theta u}{\gamma} sin ( \frac{\gamma t}{2} ) \right) \
\displaystyle B(t) & = - \frac{u - u^2}{\gamma coth ( \frac{\gamma t}{2} ) - \xi - \rho \theta u }
\end{align*}
with $ \gamma = \displaystyle \sqrt{\theta^2 (u - u^2) + (\xi + \rho \theta u)^2} $
We have the log characteristic function:
\begin{align*}
log(\chi_{Bates}^c(u)) &= u \left( \frac{1}{log ( C(t) )} + t \lambda ( 1 - \mu_A)\right) + \frac{\xi \eta t (\xi + \rho \theta u)}{\theta^2}\
&- \frac{2 \xi \eta}{\theta^2} log \left(cosh ( \frac{\gamma t}{2}) - \frac{\xi + \rho \theta u}{\gamma} sin ( \frac{\gamma t}{2} ) \right)
- V_0 \frac{u - u^2}{\gamma coth ( \frac{\gamma t}{2} ) - \xi - \rho \theta u } + u X_0 \end{align*}
and the call price in the Bates model is given by:
\begin{align*}
Call(0, S, K, t) &= C_M(0, S, K, t)\
& - \frac{K}{\pi C(t)} \displaystyle \int\limits_{0}^{\infty} Re \left[ \frac{e^{-k( \alpha + i u )}
\chi_J (\alpha + i u) }{(i u + \alpha) (i u + \alpha -1)} \left( \chi_{Heston}(\alpha + i u) - \chi_{BS}(\alpha + i u) \right) \right] du
\end{align*}
Control variate choice
To compute the Bates' call price, we can choose the Merton, Black-Scholes, or no control variate to increase the accuracy.
Remark:
Using a Black-Scholes or Merton call price as control variate, we have to choose the volatility $ \sigma $ parameter.
- Let's identify $\sigma$ by choosing $\theta = 0$. We have $ \forall t \in \mathbb{R}^{+*} $: \begin{align*} \displaystyle d( e^{\xi t} V_t ) & = V_t \xi e^{\xi t} dt + e^{\xi t} dV_t = V_t \xi e^{\xi t} dt + e^{\xi t} \xi (\eta - V_{t}) dt =e^{\xi t} \xi \eta dt \\ \displaystyle e^{\xi t} V_t - V_0 & = \int\limits_0^t e^{\xi t} \xi \eta dt \iff V_t = e^{-\xi t} (V_0 - \eta) + \eta \end{align*}
- $ \sigma $ can be chosen as the squared root of the terminal expected variance: \[ \sigma = \displaystyle \sqrt{e^{-\xi t} (V_0 - \eta) + \eta} \]
- $\sigma$ can be chosen as the squared root of the integrated variance without noise: \[ \sigma^2 = \displaystyle \int\limits_0^t V_s ds = \frac{1}{t} [ \frac{(e^{-\xi t} - 1)(\eta - V_0)}{\xi} +\eta t ] \iff \sigma = \sqrt{\frac{(e^{-\xi t} - 1)(\eta - V_0)}{\xi t} +\eta} \]
Calibration methods
We develop two calibration methods for the Bates model:
- In one step and using weight functions
- In two steps: Firstly a set of parameters is found using Merton and Heston calibration and secondly a local optimisation is performed
One step method
We minimise the imply/model volatilities in $L^2$ norm, as explain in the Merton calibration section. Let's define a weight function applied respectively to strikes and to maturities.- Weight function for strikes:
$ \forall x \in \mathbb{R}^{+*}, $ $ f(x) = \displaystyle \frac{ e^{ - \left( \frac{(x - \mu)}{\sigma} \right)^2 }}{\sigma \sqrt{2 \pi}} $ with $\mu = S_0 C(t) $, $ \sigma = scale \times \sqrt{ \frac{1}{2}(k_{min}^2 + k_{max}^2) - \frac{1}{4} (k_{min} + k_{max} )^2 } $
$ k_{min} $ minimum strike and $ k_{max} $ maximum strike for a fixed $ T \in \mathbb{R}^{+*} $ and $ scale \in \mathbb{R}^{+*} $ a scale factor - Weight function for maturities:
$ \forall x \in \mathbb{R}^{+*}, $ $ f(x) = \displaystyle (\frac{x}{x_0})^{p x_0} e^{ p(x-x_0) } $ with $ x_0 $ the centered maturity and $p$ the bandwidth
Two steps method
We inspect a first solution in the set of Bates parameters.
For the height parameters, we have:
- For $\lambda$, $\mu_z$, $\sigma_z$ and $\sigma$:
We calibrate those parameters in the Merton model for maturities lower than one year. Remark that $\sigma$ is the volatility in the Merton model and not a Bates parameter - For $V_0$, $\xi$, $\nu$, $\theta$ and $\rho$:
We calibrate those parameters in the Heston model for maturities greater than one year. Remark that $v_0$ can be taken equals to $ \sigma^2 $
The second step use the previously found parameters as initial solution for a local minimisation.
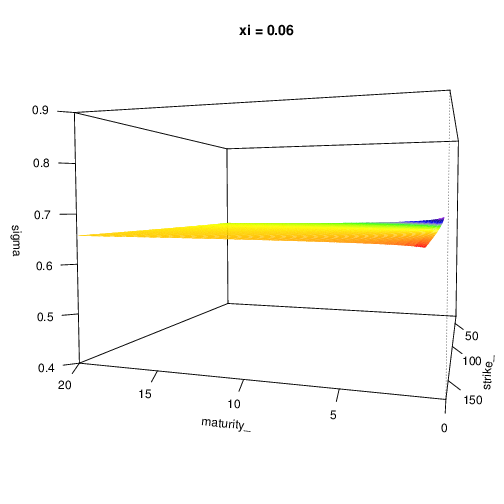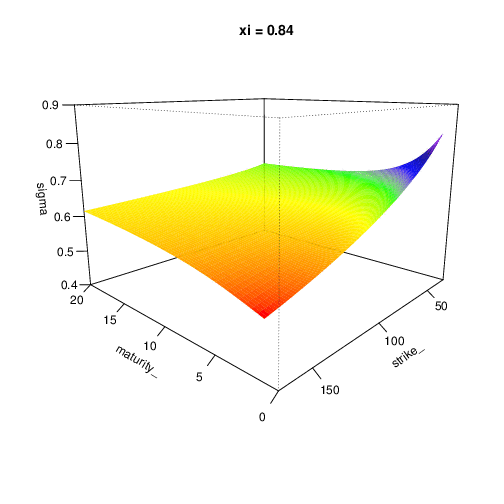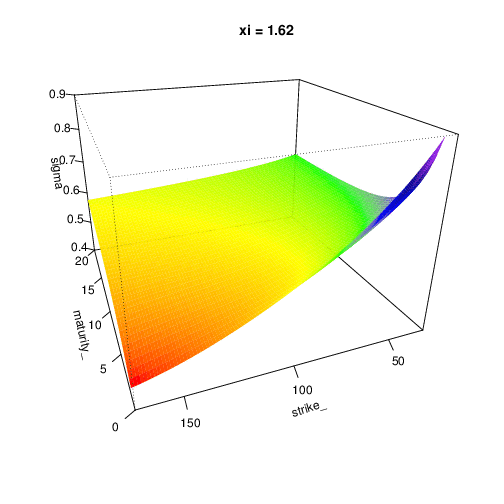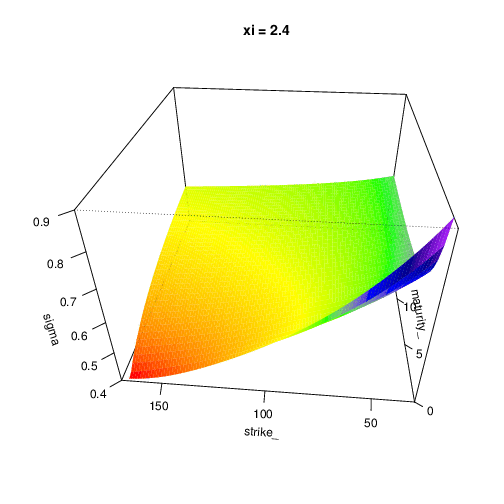
Parameters impact
To expose the parameters influence, we expose the implied volatility surface in function of the model parameters. Don’t hesitate to expand this section
Let’s have the following parameters:
- s0 = 100
- r = 0.2
- lambda = 0.5
- v0 = 0.4
- mu_z = -0.2
- sigma_z = 0.2
- kappa = 0.5
- theta = 0.4
- xi = 0.9
- rho = -0.7
Conclusion
We presented in this post some theoretical aspects on discontinuous processes. We also exposed a generic formulation for jump diffusion model using Lévy process. We investigated two specific models: Merton and Bates models. The dynamic, call pricing, calibration and influence of parameters are exposed for each models. Numerical experiments are provided.
This methodology has been chosen to be implemented in LexiFi Apropos.